The topic of this article is the calculation of a polycarbonate canopy with your own hands. We have to learn how to calculate the main parameters of the structure associated with its strength and dimensions. So, let's go.

What do we calculate
We have to learn how to calculate:
- The thickness of the polycarbonate and the pitch of the crate depending on the expected snow load per square meter.
- Arch cover dimensions (which in terms of geometry comes down to calculating the length of the arc).
To clarify: we are exploring ways to calculate the arc for known radius and angle of the sector, as well as for the case when we know only the distances between the extreme points of the arch surface.
- Minimum pipe section with a known bending load.
In this order, we will move on.
Lathing and coating thickness
Let's start with the calculation of the snow load.
Before we figure out how to calculate a polycarbonate canopy, we will formulate a couple of assumptions on which the calculation is based.
- The given data are relevant for high-quality material without signs of destruction by ultraviolet radiation. Polycarbonate without a UV filter becomes brittle after 2-3 years of operation in the light.

- We deliberately neglect the limited deformation stability of the crate, considering it to be absolutely strong.
And now - a table that will help you choose the optimal thickness of polycarbonate and the pitch of the crate.
| Load, kg/m2 | Crate cell dimensions with polycarbonate thickness, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200x900 | 1320x920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880x660 | 1000x750 | 1050x750 | 1150x900 |
| 760x760 | 830x830 | 830x830 | 970x970 | |
| 700x860 | 750x900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950x700 | 1100x850 |
| 690x690 | 760x760 | 780x780 | 880x880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
Arch
Calculation by radius and sector
How to calculate the arch for a canopy if we know the bending radius and arc sector?

The formula will look like P=pi*r*n/180, where:
- P is the length of the arc (in our case, the length of a polycarbonate sheet or a profile pipe, which will become an element of the frame).
- pi is the number "pi" (in calculations that do not require extremely high accuracy, usually taken equal to 3.14).
- r is the radius of the arc.
- n is the arc angle in degrees.
Let's, as an example, calculate with our own hands the length of the canopy arch with a radius of 2 meters and a sector of 35 degrees.
P \u003d 3.14 * 2 * 35 / 180 \u003d 1.22 meters.
In the process of work, the opposite situation often arises: it is necessary to adjust the radius and sector of the arc to a fixed length of the arch. The reasons are clear: the price of polycarbonate is high enough to minimize the amount of waste.
Obviously, in this case the product of the sector and the radius will be equal to P/pi*180.
Let's try to fit the arch under a standard sheet 6 meters long. 6/3.14*180=343.9 (with rounding). Further - a simple selection of values \u200b\u200bwith a calculator in hand: for example, for an arc sector of 180 degrees, you can take the radius equal to 343.9 / 180 \u003d 1.91 meters; with a radius of 2 meters, the sector will be equal to 343.9 / 2 \u003d 171.95 degrees.
Calculation by chords
What does the calculation of the design of a polycarbonate canopy with an arch look like if we only have information about the distance between the edges of the arch and its height?
In this case, the so-called Huygens formula is applied. To use it, let's mentally divide the chord connecting the ends of the arch in half, after which we draw a perpendicular to the chord in the middle.
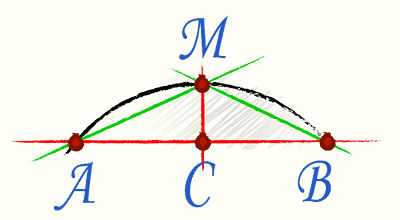
The formula itself has the form Р=2l+1/3*(2l-L), where l is the AM chord and L is the AB chord.
Important: the calculation gives an approximate result. The maximum error is 0.5%; the smaller the angular sector of the arch, the smaller the error.
Let's calculate the length of the arch for the case when AB \u003d 2 m and AM - 1.2 m.
P=2*1.2+1/3*(2*1.2-2)=2.4+1/3*0.4=2.533 meters.
Calculation of the section with a known bending load
Quite a life situation: part of the canopy is a visor of known length. We can roughly estimate the peak snow load on it. How to choose a profile pipe of such a section for beams so that it does not bend under load?

Note! We deliberately do not touch on how to calculate the load on the canopy. Assessment of snow and wind load is a completely self-sufficient topic for a separate article.
To calculate, we need two formulas:
- M = FL, where M is the bending moment, F is the force applied to the end of the lever in kilograms (in our case, the weight of the snow on the visor), and L is the length of the lever (the length of the beam that bears the load from the snow, from edge to point fasteners) in centimeters.
- M/W=R, where W is the moment of resistance and R is the strength of the material.
And how will this heap of unknown values help us?
By itself, nothing. Some reference data is missing for the calculation.
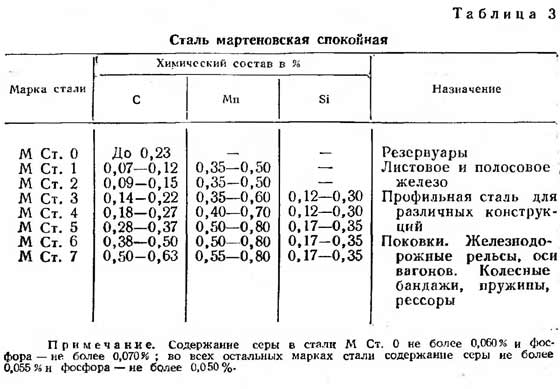
| steel grade | Strength (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Reference: St3, St4 and St5 steels are usually used for professional pipes.
Now, based on the data we have, we can calculate the bending resistance moment of the profile pipe. Let's do that.
Suppose that 400 kilograms of snow accumulate on a two-meter canopy with three bearing beams made of St3 steel.To simplify the calculations, we will agree that the entire load falls on the edge of the visor. Obviously, the load on each beam will be 400/3=133.3 kg; with a two-meter lever, the bending moment will be equal to 133.3 * 200 \u003d 26660 kgf * cm.
Now we calculate the moment of resistance W. From the equation 26660 kgf * cm / W = 2100 kgf / cm2 (strength of steel) it follows that the moment of resistance should be at least 26660 kgf * cm / 2100 kgf / cm2 = 12.7 cm3.
How will the value of the moment of resistance lead us to the dimensions of the pipe? Through the assortment tables contained in GOST 8639-82 and GOST 8645-68 regulating the dimensions of square and shaped pipes. For each size, they indicate the corresponding moment of resistance, and for a rectangular section - along each of the axes.
After checking the tables, we find out that the minimum size of a square pipe with the required characteristics is 50x50x7.0 mm; rectangular (with vertical orientation of the larger side) - 70x30x5.0 mm.

Conclusion
We hope that we have not overworked the reader with an abundance of dry figures and formulas. As always, additional information on the methods for calculating and designing polycarbonate canopies can be found in the video in this article. Good luck!
Did the article help you?